Limit cycles

In contrast to the previous tutorials, limit cycle problems feature harmonic(s) whose numerical value is not imposed externally. We shall construct our HarmonicEquation as usual, but identify this harmonic as an extra variable, rather than a fixed parameter.

Non-driven system - the van der Pol oscillator

Here we solve the equation of motion of the van der Pol oscillator. This is a single-variable second-order ODE with continuous time-translation symmetry (i.e., no 'clock' imposing a frequency and/or phase), which displays periodic solutions known as relaxation oscillations. For more detail, refer also to arXiv:2308.06092.

using HarmonicBalance
@variables ω_lc, t, ω0, x(t), μ
diff_eq = DifferentialEquation(d(d(x,t),t) - μ*(1-x^2) * d(x,t) + x, x)

System of 1 differential equations
Variables:       x(t)
Harmonic ansatz: x(t) => ;   

x(t) + Differential(t)(Differential(t)(x(t))) - (1 - (x(t)^2))*Differential(t)(x(t))*μ ~ 0

Choosing to expand the motion of $x(t)$ using ${\omega }_{lc}$, $3{\omega }_{lc}$ and $5{\omega }_{lc}$, we define

foreach(1:2:5) do i
  add_harmonic!(diff_eq, x, i*ω_lc)
end;

and obtain 6 harmonic equations,

harmonic_eq = get_harmonic_equations(diff_eq)

A set of 6 harmonic equations
Variables: u1(T), v1(T), u2(T), v2(T), u3(T), v3(T)
Parameters: ω_lc, μ

Harmonic ansatz: 
x(t) = u1(T)*cos(ω_lct) + v1(T)*sin(ω_lct) + u2(T)*cos(3ω_lct) + v2(T)*sin(3ω_lct) + u3(T)*cos(5ω_lct) + v3(T)*sin(5ω_lct)

Harmonic equations:

u1(T) + (2//1)*Differential(T)(v1(T))*ω_lc - Differential(T)(u1(T))*μ - u1(T)*(ω_lc^2) - v1(T)*μ*ω_lc + (1//4)*(u1(T)^2)*Differential(T)(u2(T))*μ + (3//4)*(u1(T)^2)*Differential(T)(u1(T))*μ + u1(T)*Differential(T)(u3(T))*u3(T)*μ + (1//2)*u1(T)*Differential(T)(u3(T))*u2(T)*μ + u1(T)*Differential(T)(v3(T))*v3(T)*μ + (1//2)*u1(T)*Differential(T)(v3(T))*v2(T)*μ + (1//2)*u1(T)*v3(T)*Differential(T)(v2(T))*μ + (1//2)*u1(T)*Differential(T)(v1(T))*v2(T)*μ + (1//2)*u1(T)*Differential(T)(v1(T))*v1(T)*μ + u1(T)*v2(T)*Differential(T)(v2(T))*μ + (1//2)*u1(T)*v1(T)*Differential(T)(v2(T))*μ + (1//2)*u1(T)*Differential(T)(u2(T))*u3(T)*μ + u1(T)*Differential(T)(u2(T))*u2(T)*μ + (1//2)*u1(T)*Differential(T)(u1(T))*u2(T)*μ - (1//4)*Differential(T)(u3(T))*(v2(T)^2)*μ - (1//2)*Differential(T)(u3(T))*v2(T)*v1(T)*μ + (1//4)*Differential(T)(u3(T))*(u2(T)^2)*μ + (1//2)*Differential(T)(v3(T))*v2(T)*u2(T)*μ + (1//2)*Differential(T)(v3(T))*v1(T)*u2(T)*μ + (1//2)*(v3(T)^2)*Differential(T)(u1(T))*μ + (1//2)*v3(T)*Differential(T)(v1(T))*u2(T)*μ + (1//2)*v3(T)*v2(T)*Differential(T)(u2(T))*μ + (1//2)*v3(T)*v2(T)*Differential(T)(u1(T))*μ + (1//2)*v3(T)*v1(T)*Differential(T)(u2(T))*μ + (1//2)*v3(T)*u2(T)*Differential(T)(v2(T))*μ - (1//2)*Differential(T)(v1(T))*v2(T)*u3(T)*μ - (1//2)*Differential(T)(v1(T))*v1(T)*u2(T)*μ + (1//2)*(v2(T)^2)*Differential(T)(u1(T))*μ + (1//2)*v2(T)*v1(T)*Differential(T)(u1(T))*μ - (1//2)*v2(T)*u3(T)*Differential(T)(v2(T))*μ - (1//4)*(v1(T)^2)*Differential(T)(u2(T))*μ + (1//4)*(v1(T)^2)*Differential(T)(u1(T))*μ - (1//2)*v1(T)*u3(T)*Differential(T)(v2(T))*μ + (1//2)*Differential(T)(u2(T))*u3(T)*u2(T)*μ + (1//2)*(u3(T)^2)*Differential(T)(u1(T))*μ + (1//2)*u3(T)*Differential(T)(u1(T))*u2(T)*μ + (1//2)*Differential(T)(u1(T))*(u2(T)^2)*μ + (1//4)*(u1(T)^2)*v2(T)*μ*ω_lc + (1//4)*(u1(T)^2)*v1(T)*μ*ω_lc + (1//2)*u1(T)*v3(T)*u2(T)*μ*ω_lc - (1//2)*u1(T)*v2(T)*u3(T)*μ*ω_lc - (1//2)*u1(T)*v1(T)*u2(T)*μ*ω_lc + (1//2)*(v3(T)^2)*v1(T)*μ*ω_lc + (1//4)*v3(T)*(v2(T)^2)*μ*ω_lc - (1//2)*v3(T)*v2(T)*v1(T)*μ*ω_lc - (1//4)*v3(T)*(u2(T)^2)*μ*ω_lc + (1//2)*(v2(T)^2)*v1(T)*μ*ω_lc - (1//4)*v2(T)*(v1(T)^2)*μ*ω_lc + (1//2)*v2(T)*u3(T)*u2(T)*μ*ω_lc + (1//4)*(v1(T)^3)*μ*ω_lc + (1//2)*v1(T)*(u3(T)^2)*μ*ω_lc - (1//2)*v1(T)*u3(T)*u2(T)*μ*ω_lc + (1//2)*v1(T)*(u2(T)^2)*μ*ω_lc ~ 0

v1(T) - Differential(T)(v1(T))*μ - (2//1)*Differential(T)(u1(T))*ω_lc + u1(T)*μ*ω_lc - v1(T)*(ω_lc^2) + (1//4)*(u1(T)^2)*Differential(T)(v1(T))*μ + (1//4)*(u1(T)^2)*Differential(T)(v2(T))*μ - (1//2)*u1(T)*Differential(T)(u3(T))*v2(T)*μ + (1//2)*u1(T)*Differential(T)(v3(T))*u2(T)*μ + (1//2)*u1(T)*v3(T)*Differential(T)(u2(T))*μ - (1//2)*u1(T)*Differential(T)(v1(T))*u2(T)*μ + (1//2)*u1(T)*v2(T)*Differential(T)(u1(T))*μ - (1//2)*u1(T)*v1(T)*Differential(T)(u2(T))*μ + (1//2)*u1(T)*v1(T)*Differential(T)(u1(T))*μ - (1//2)*u1(T)*u3(T)*Differential(T)(v2(T))*μ + (1//2)*Differential(T)(u3(T))*v2(T)*u2(T)*μ + Differential(T)(u3(T))*v1(T)*u3(T)*μ - (1//2)*Differential(T)(u3(T))*v1(T)*u2(T)*μ + Differential(T)(v3(T))*v3(T)*v1(T)*μ + (1//4)*Differential(T)(v3(T))*(v2(T)^2)*μ - (1//2)*Differential(T)(v3(T))*v2(T)*v1(T)*μ - (1//4)*Differential(T)(v3(T))*(u2(T)^2)*μ + (1//2)*(v3(T)^2)*Differential(T)(v1(T))*μ - (1//2)*v3(T)*Differential(T)(v1(T))*v2(T)*μ + (1//2)*v3(T)*v2(T)*Differential(T)(v2(T))*μ - (1//2)*v3(T)*v1(T)*Differential(T)(v2(T))*μ - (1//2)*v3(T)*Differential(T)(u2(T))*u2(T)*μ + (1//2)*v3(T)*Differential(T)(u1(T))*u2(T)*μ + (1//2)*Differential(T)(v1(T))*(v2(T)^2)*μ - (1//2)*Differential(T)(v1(T))*v2(T)*v1(T)*μ + (3//4)*Differential(T)(v1(T))*(v1(T)^2)*μ + (1//2)*Differential(T)(v1(T))*(u3(T)^2)*μ - (1//2)*Differential(T)(v1(T))*u3(T)*u2(T)*μ + (1//2)*Differential(T)(v1(T))*(u2(T)^2)*μ + v2(T)*v1(T)*Differential(T)(v2(T))*μ + (1//2)*v2(T)*Differential(T)(u2(T))*u3(T)*μ - (1//2)*v2(T)*u3(T)*Differential(T)(u1(T))*μ - (1//4)*(v1(T)^2)*Differential(T)(v2(T))*μ - (1//2)*v1(T)*Differential(T)(u2(T))*u3(T)*μ + v1(T)*Differential(T)(u2(T))*u2(T)*μ - (1//2)*v1(T)*Differential(T)(u1(T))*u2(T)*μ + (1//2)*u3(T)*u2(T)*Differential(T)(v2(T))*μ - (1//4)*(u1(T)^3)*μ*ω_lc - (1//4)*(u1(T)^2)*u2(T)*μ*ω_lc - (1//2)*u1(T)*(v3(T)^2)*μ*ω_lc - (1//2)*u1(T)*v3(T)*v2(T)*μ*ω_lc - (1//2)*u1(T)*(v2(T)^2)*μ*ω_lc - (1//2)*u1(T)*v2(T)*v1(T)*μ*ω_lc - (1//4)*u1(T)*(v1(T)^2)*μ*ω_lc - (1//2)*u1(T)*(u3(T)^2)*μ*ω_lc - (1//2)*u1(T)*u3(T)*u2(T)*μ*ω_lc - (1//2)*u1(T)*(u2(T)^2)*μ*ω_lc - (1//2)*v3(T)*v2(T)*u2(T)*μ*ω_lc - (1//2)*v3(T)*v1(T)*u2(T)*μ*ω_lc + (1//4)*(v2(T)^2)*u3(T)*μ*ω_lc + (1//2)*v2(T)*v1(T)*u3(T)*μ*ω_lc + (1//4)*(v1(T)^2)*u2(T)*μ*ω_lc - (1//4)*u3(T)*(u2(T)^2)*μ*ω_lc ~ 0

u2(T) - Differential(T)(u2(T))*μ + (6//1)*Differential(T)(v2(T))*ω_lc - (3//1)*v2(T)*μ*ω_lc - (9//1)*u2(T)*(ω_lc^2) + (1//4)*(u1(T)^2)*Differential(T)(u3(T))*μ + (1//2)*(u1(T)^2)*Differential(T)(u2(T))*μ + (1//4)*(u1(T)^2)*Differential(T)(u1(T))*μ + (1//2)*u1(T)*Differential(T)(u3(T))*u2(T)*μ + (1//2)*u1(T)*Differential(T)(v3(T))*v2(T)*μ + (1//2)*u1(T)*Differential(T)(v3(T))*v1(T)*μ + (1//2)*u1(T)*v3(T)*Differential(T)(v1(T))*μ + (1//2)*u1(T)*v3(T)*Differential(T)(v2(T))*μ - (1//2)*u1(T)*Differential(T)(v1(T))*v1(T)*μ + (1//2)*u1(T)*Differential(T)(u2(T))*u3(T)*μ + (1//2)*u1(T)*u3(T)*Differential(T)(u1(T))*μ + u1(T)*Differential(T)(u1(T))*u2(T)*μ + (1//2)*Differential(T)(u3(T))*v2(T)*v1(T)*μ - (1//4)*Differential(T)(u3(T))*(v1(T)^2)*μ + Differential(T)(u3(T))*u3(T)*u2(T)*μ + Differential(T)(v3(T))*v3(T)*u2(T)*μ - (1//2)*Differential(T)(v3(T))*v1(T)*u2(T)*μ + (1//2)*(v3(T)^2)*Differential(T)(u2(T))*μ - (1//2)*v3(T)*Differential(T)(v1(T))*u2(T)*μ + (1//2)*v3(T)*v2(T)*Differential(T)(u1(T))*μ - (1//2)*v3(T)*v1(T)*Differential(T)(u2(T))*μ + (1//2)*v3(T)*v1(T)*Differential(T)(u1(T))*μ + (1//2)*Differential(T)(v1(T))*v2(T)*u3(T)*μ - (1//2)*Differential(T)(v1(T))*v1(T)*u3(T)*μ + Differential(T)(v1(T))*v1(T)*u2(T)*μ + (1//4)*(v2(T)^2)*Differential(T)(u2(T))*μ + (1//2)*v2(T)*u2(T)*Differential(T)(v2(T))*μ + (1//2)*(v1(T)^2)*Differential(T)(u2(T))*μ - (1//4)*(v1(T)^2)*Differential(T)(u1(T))*μ + (1//2)*v1(T)*u3(T)*Differential(T)(v2(T))*μ + (1//2)*Differential(T)(u2(T))*(u3(T)^2)*μ + (3//4)*Differential(T)(u2(T))*(u2(T)^2)*μ + (1//2)*u3(T)*Differential(T)(u1(T))*u2(T)*μ + (3//4)*(u1(T)^2)*v3(T)*μ*ω_lc + (3//2)*(u1(T)^2)*v2(T)*μ*ω_lc + (3//4)*(u1(T)^2)*v1(T)*μ*ω_lc + (3//2)*u1(T)*v3(T)*u2(T)*μ*ω_lc - (3//2)*u1(T)*v2(T)*u3(T)*μ*ω_lc - (3//2)*u1(T)*v1(T)*u3(T)*μ*ω_lc + (3//2)*(v3(T)^2)*v2(T)*μ*ω_lc + (3//2)*v3(T)*v2(T)*v1(T)*μ*ω_lc - (3//4)*v3(T)*(v1(T)^2)*μ*ω_lc + (3//4)*(v2(T)^3)*μ*ω_lc + (3//2)*v2(T)*(v1(T)^2)*μ*ω_lc + (3//2)*v2(T)*(u3(T)^2)*μ*ω_lc + (3//4)*v2(T)*(u2(T)^2)*μ*ω_lc - (1//4)*(v1(T)^3)*μ*ω_lc + (3//2)*v1(T)*u3(T)*u2(T)*μ*ω_lc ~ 0

v2(T) - (6//1)*Differential(T)(u2(T))*ω_lc - Differential(T)(v2(T))*μ - (9//1)*v2(T)*(ω_lc^2) + (3//1)*u2(T)*μ*ω_lc + (1//4)*(u1(T)^2)*Differential(T)(v3(T))*μ + (1//4)*(u1(T)^2)*Differential(T)(v1(T))*μ + (1//2)*(u1(T)^2)*Differential(T)(v2(T))*μ - (1//2)*u1(T)*Differential(T)(u3(T))*v2(T)*μ - (1//2)*u1(T)*Differential(T)(u3(T))*v1(T)*μ + (1//2)*u1(T)*Differential(T)(v3(T))*u2(T)*μ + (1//2)*u1(T)*v3(T)*Differential(T)(u2(T))*μ + (1//2)*u1(T)*v3(T)*Differential(T)(u1(T))*μ - (1//2)*u1(T)*Differential(T)(v1(T))*u3(T)*μ + u1(T)*v2(T)*Differential(T)(u1(T))*μ + (1//2)*u1(T)*v1(T)*Differential(T)(u1(T))*μ - (1//2)*u1(T)*u3(T)*Differential(T)(v2(T))*μ + Differential(T)(u3(T))*v2(T)*u3(T)*μ + (1//2)*Differential(T)(u3(T))*v1(T)*u2(T)*μ + Differential(T)(v3(T))*v3(T)*v2(T)*μ + (1//2)*Differential(T)(v3(T))*v2(T)*v1(T)*μ - (1//4)*Differential(T)(v3(T))*(v1(T)^2)*μ + (1//2)*(v3(T)^2)*Differential(T)(v2(T))*μ + (1//2)*v3(T)*Differential(T)(v1(T))*v2(T)*μ - (1//2)*v3(T)*Differential(T)(v1(T))*v1(T)*μ + (1//2)*v3(T)*v1(T)*Differential(T)(v2(T))*μ + (1//2)*v3(T)*Differential(T)(u1(T))*u2(T)*μ + Differential(T)(v1(T))*v2(T)*v1(T)*μ - (1//4)*Differential(T)(v1(T))*(v1(T)^2)*μ + (1//2)*Differential(T)(v1(T))*u3(T)*u2(T)*μ + (3//4)*(v2(T)^2)*Differential(T)(v2(T))*μ + (1//2)*v2(T)*Differential(T)(u2(T))*u2(T)*μ - (1//2)*v2(T)*u3(T)*Differential(T)(u1(T))*μ + (1//2)*(v1(T)^2)*Differential(T)(v2(T))*μ + (1//2)*v1(T)*Differential(T)(u2(T))*u3(T)*μ - (1//2)*v1(T)*u3(T)*Differential(T)(u1(T))*μ + (1//2)*(u3(T)^2)*Differential(T)(v2(T))*μ + (1//4)*(u2(T)^2)*Differential(T)(v2(T))*μ - (1//4)*(u1(T)^3)*μ*ω_lc - (3//4)*(u1(T)^2)*u3(T)*μ*ω_lc - (3//2)*(u1(T)^2)*u2(T)*μ*ω_lc - (3//2)*u1(T)*v3(T)*v2(T)*μ*ω_lc - (3//2)*u1(T)*v3(T)*v1(T)*μ*ω_lc + (3//4)*u1(T)*(v1(T)^2)*μ*ω_lc - (3//2)*u1(T)*u3(T)*u2(T)*μ*ω_lc - (3//2)*(v3(T)^2)*u2(T)*μ*ω_lc + (3//2)*v3(T)*v1(T)*u2(T)*μ*ω_lc - (3//4)*(v2(T)^2)*u2(T)*μ*ω_lc - (3//2)*v2(T)*v1(T)*u3(T)*μ*ω_lc + (3//4)*(v1(T)^2)*u3(T)*μ*ω_lc - (3//2)*(v1(T)^2)*u2(T)*μ*ω_lc - (3//2)*(u3(T)^2)*u2(T)*μ*ω_lc - (3//4)*(u2(T)^3)*μ*ω_lc ~ 0

u3(T) - Differential(T)(u3(T))*μ + (10//1)*Differential(T)(v3(T))*ω_lc - (5//1)*v3(T)*μ*ω_lc - (25//1)*u3(T)*(ω_lc^2) + (1//2)*(u1(T)^2)*Differential(T)(u3(T))*μ + (1//4)*(u1(T)^2)*Differential(T)(u2(T))*μ - (1//2)*u1(T)*Differential(T)(v1(T))*v2(T)*μ - (1//2)*u1(T)*v2(T)*Differential(T)(v2(T))*μ - (1//2)*u1(T)*v1(T)*Differential(T)(v2(T))*μ + (1//2)*u1(T)*Differential(T)(u2(T))*u2(T)*μ + u1(T)*u3(T)*Differential(T)(u1(T))*μ + (1//2)*u1(T)*Differential(T)(u1(T))*u2(T)*μ + (1//4)*Differential(T)(u3(T))*(v3(T)^2)*μ + (1//2)*Differential(T)(u3(T))*(v2(T)^2)*μ + (1//2)*Differential(T)(u3(T))*(v1(T)^2)*μ + (3//4)*Differential(T)(u3(T))*(u3(T)^2)*μ + (1//2)*Differential(T)(u3(T))*(u2(T)^2)*μ + (1//2)*Differential(T)(v3(T))*v3(T)*u3(T)*μ + (1//2)*Differential(T)(v1(T))*v2(T)*u2(T)*μ + Differential(T)(v1(T))*v1(T)*u3(T)*μ - (1//2)*Differential(T)(v1(T))*v1(T)*u2(T)*μ - (1//4)*(v2(T)^2)*Differential(T)(u1(T))*μ + (1//2)*v2(T)*v1(T)*Differential(T)(u2(T))*μ - (1//2)*v2(T)*v1(T)*Differential(T)(u1(T))*μ + v2(T)*u3(T)*Differential(T)(v2(T))*μ - (1//4)*(v1(T)^2)*Differential(T)(u2(T))*μ + (1//2)*v1(T)*u2(T)*Differential(T)(v2(T))*μ + Differential(T)(u2(T))*u3(T)*u2(T)*μ + (1//4)*Differential(T)(u1(T))*(u2(T)^2)*μ + (5//2)*(u1(T)^2)*v3(T)*μ*ω_lc + (5//4)*(u1(T)^2)*v2(T)*μ*ω_lc + (5//2)*u1(T)*v2(T)*u2(T)*μ*ω_lc + (5//2)*u1(T)*v1(T)*u2(T)*μ*ω_lc + (5//4)*(v3(T)^3)*μ*ω_lc + (5//2)*v3(T)*(v2(T)^2)*μ*ω_lc + (5//2)*v3(T)*(v1(T)^2)*μ*ω_lc + (5//4)*v3(T)*(u3(T)^2)*μ*ω_lc + (5//2)*v3(T)*(u2(T)^2)*μ*ω_lc + (5//4)*(v2(T)^2)*v1(T)*μ*ω_lc - (5//4)*v2(T)*(v1(T)^2)*μ*ω_lc - (5//4)*v1(T)*(u2(T)^2)*μ*ω_lc ~ 0

v3(T) - (10//1)*Differential(T)(u3(T))*ω_lc - Differential(T)(v3(T))*μ - (25//1)*v3(T)*(ω_lc^2) + (5//1)*u3(T)*μ*ω_lc + (1//2)*(u1(T)^2)*Differential(T)(v3(T))*μ + (1//4)*(u1(T)^2)*Differential(T)(v2(T))*μ + u1(T)*v3(T)*Differential(T)(u1(T))*μ + (1//2)*u1(T)*Differential(T)(v1(T))*u2(T)*μ + (1//2)*u1(T)*v2(T)*Differential(T)(u2(T))*μ + (1//2)*u1(T)*v2(T)*Differential(T)(u1(T))*μ + (1//2)*u1(T)*v1(T)*Differential(T)(u2(T))*μ + (1//2)*u1(T)*u2(T)*Differential(T)(v2(T))*μ + (1//2)*Differential(T)(u3(T))*v3(T)*u3(T)*μ + (3//4)*Differential(T)(v3(T))*(v3(T)^2)*μ + (1//2)*Differential(T)(v3(T))*(v2(T)^2)*μ + (1//2)*Differential(T)(v3(T))*(v1(T)^2)*μ + (1//4)*Differential(T)(v3(T))*(u3(T)^2)*μ + (1//2)*Differential(T)(v3(T))*(u2(T)^2)*μ + v3(T)*Differential(T)(v1(T))*v1(T)*μ + v3(T)*v2(T)*Differential(T)(v2(T))*μ + v3(T)*Differential(T)(u2(T))*u2(T)*μ + (1//4)*Differential(T)(v1(T))*(v2(T)^2)*μ - (1//2)*Differential(T)(v1(T))*v2(T)*v1(T)*μ - (1//4)*Differential(T)(v1(T))*(u2(T)^2)*μ + (1//2)*v2(T)*v1(T)*Differential(T)(v2(T))*μ + (1//2)*v2(T)*Differential(T)(u1(T))*u2(T)*μ - (1//4)*(v1(T)^2)*Differential(T)(v2(T))*μ - (1//2)*v1(T)*Differential(T)(u2(T))*u2(T)*μ + (1//2)*v1(T)*Differential(T)(u1(T))*u2(T)*μ - (5//2)*(u1(T)^2)*u3(T)*μ*ω_lc - (5//4)*(u1(T)^2)*u2(T)*μ*ω_lc + (5//4)*u1(T)*(v2(T)^2)*μ*ω_lc + (5//2)*u1(T)*v2(T)*v1(T)*μ*ω_lc - (5//4)*u1(T)*(u2(T)^2)*μ*ω_lc - (5//4)*(v3(T)^2)*u3(T)*μ*ω_lc - (5//2)*(v2(T)^2)*u3(T)*μ*ω_lc - (5//2)*v2(T)*v1(T)*u2(T)*μ*ω_lc - (5//2)*(v1(T)^2)*u3(T)*μ*ω_lc + (5//4)*(v1(T)^2)*u2(T)*μ*ω_lc - (5//4)*(u3(T)^3)*μ*ω_lc - (5//2)*u3(T)*(u2(T)^2)*μ*ω_lc ~ 0

So far, ${\omega }_{lc}$ appears as any other harmonic. However, it is not fixed by any external drive or 'clock', instead, it emerges out of a Hopf instability in the system. We can verify that fixing ω_lc and calling get_steady_states.

get_steady_states(harmonic_eq, μ => 1:0.1:5, ω_lc => 1.2)

gives a single solution with zero amplitude.

Taking instead ${\omega }_{lc}$ as a variable to be solved for results in a phase freedom, implying an infinite number of solutions. To perform the gauge-fixing procedure, we call get_limit_cycles, marking the limit cycle harmonic as a keyword argument,

result = get_limit_cycles(harmonic_eq, μ => 1:0.1:5, (), ω_lc)

A steady state result for 41 parameter points

Solution branches:   92
   of which real:    4
   of which stable:  4

Classes: unique_cycle, stable, physical, Hopf, binary_labels

The results show a fourfold degeneracy of solutions:

plot(result, y="ω_lc")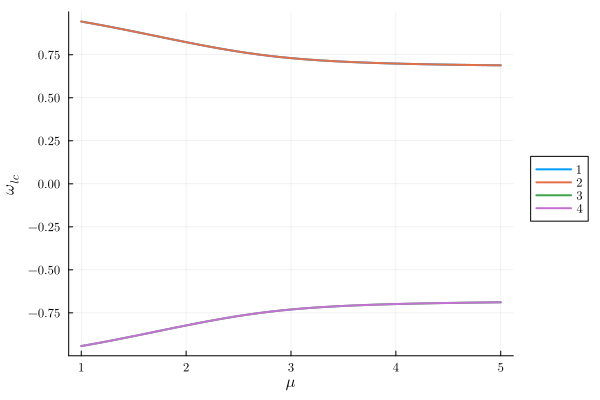

The automatically created solution class unique_cycle filters the degeneracy out:

plot(result, y="ω_lc", class="unique_cycle")

Driven system - coupled Duffings

So far, we have largely focused on finding and analysing steady states, i.e., fixed points of the harmonic equations, which satisfy

$$\frac{d\mathbf{u}(T)}{dT}=\overline{\mathbf{F}}(\mathbf{u})=0.$$

Fixed points are however merely a subset of possible solutions of Eq. \eqref{eq:harmeqfull} – strictly speaking, solutions where $\mathbf{u}(T)$ remains time-dependent are allowed. These are quite unusual, since $\overline{\mathbf{F}}(\mathbf{u})$ is by construction time-independent and Eq. \eqref{eq:harmeqfull} thus possesses continuous time-translation symmetry. The appearance of explicitly time-dependent solutions then constitutes spontaneous time-translation symmetry breaking.

Such solutions, known as limit cycles, typically appear as closed periodic trajectories of the harmonic variables $\mathbf{u}(T)$. The simplest way to numerically characterise them is a time-dependent simulation, using a steady-state diagram as a guide.

Here we reconstruct the results of Zambon et al., Phys Rev. A 102, 023526 (2020), where limit cycles are shown to appear in a system of two coupled nonlinear oscillators. In this problem, two oscillators $x_1$ and $x_2$, have (the same) damping and Kerr nonlinearity and are linearly coupled,

$$\begin{array}{rl}{\ddot{x}}_1+\gamma {\dot{x}}_1+{\omega }_0^2{x}_1+\alpha x_1^3+2J(x_1-x_2)& =F_0\cos (\omega t)\\ {\ddot{x}}_2+\gamma {\dot{x}}_2+{\omega }_0^2{x}_2+\alpha x_2^3+2J(x_2-x_1)& =\eta F_0\cos (\omega t)\end{array}$$

using HarmonicBalance
@variables γ F α ω0 F0 η ω J t x(t) y(t);
eqs = [d(x,t,2) + γ*d(x,t) + ω0^2*x + α*x^3 + 2*J*ω0*(x-y) - F0*cos(ω*t),
       d(y,t,2) + γ*d(y,t) + ω0^2*y + α*y^3 + 2*J*ω0*(y-x) - η*F0*cos(ω*t)]
diff_eq = DifferentialEquation(eqs, [x,y])

System of 2 differential equations
Variables:       x(t), y(t)
Harmonic ansatz: x(t) => ;   y(t) => ;   

Differential(t)(Differential(t)(x(t))) - F0*cos(t*ω) + Differential(t)(x(t))*γ + 2J*(x(t) - y(t))*ω0 + x(t)*(ω0^2) + (x(t)^3)*α ~ 0
Differential(t)(Differential(t)(y(t))) + Differential(t)(y(t))*γ - F0*cos(t*ω)*η + 2J*(-x(t) + y(t))*ω0 + y(t)*(ω0^2) + (y(t)^3)*α ~ 0

The analysis of Zambon et al. uses a frame rotating at the pump frequency $\omega$ to describe both oscillators. For us, this means we expand both modes using $\omega$ to obtain the harmonic equations.

add_harmonic!(diff_eq, x, ω)
add_harmonic!(diff_eq, y, ω)

harmonic_eq = get_harmonic_equations(diff_eq)

A set of 4 harmonic equations
Variables: u1(T), v1(T), u2(T), v2(T)
Parameters: ω, ω0, J, α, γ, F0, η

Harmonic ansatz: 
x(t) = u1(T)*cos(ωt) + v1(T)*sin(ωt)
y(t) = u2(T)*cos(ωt) + v2(T)*sin(ωt)

Harmonic equations:

-F0 + (2//1)*Differential(T)(v1(T))*ω + Differential(T)(u1(T))*γ + (2//1)*J*u1(T)*ω0 - (2//1)*J*u2(T)*ω0 - u1(T)*(ω^2) + u1(T)*(ω0^2) + v1(T)*γ*ω + (3//4)*(u1(T)^3)*α + (3//4)*u1(T)*(v1(T)^2)*α ~ 0

Differential(T)(v1(T))*γ - (2//1)*Differential(T)(u1(T))*ω - (2//1)*J*v2(T)*ω0 + (2//1)*J*v1(T)*ω0 - u1(T)*γ*ω - v1(T)*(ω^2) + v1(T)*(ω0^2) + (3//4)*(u1(T)^2)*v1(T)*α + (3//4)*(v1(T)^3)*α ~ 0

-F0*η + Differential(T)(u2(T))*γ + (2//1)*Differential(T)(v2(T))*ω - (2//1)*J*u1(T)*ω0 + (2//1)*J*u2(T)*ω0 + v2(T)*γ*ω - u2(T)*(ω^2) + u2(T)*(ω0^2) + (3//4)*(v2(T)^2)*u2(T)*α + (3//4)*(u2(T)^3)*α ~ 0

-(2//1)*Differential(T)(u2(T))*ω + Differential(T)(v2(T))*γ + (2//1)*J*v2(T)*ω0 - (2//1)*J*v1(T)*ω0 - v2(T)*(ω^2) + v2(T)*(ω0^2) - u2(T)*γ*ω + (3//4)*(v2(T)^3)*α + (3//4)*v2(T)*(u2(T)^2)*α ~ 0

Solving for a range of drive amplitudes $F_0$,

fixed = (
    ω0 => 1.4504859, # natural frequency of separate modes (in paper's notation, ħω0 - J)
    γ => 27.4e-6,    # damping
    J => 154.1e-6,   # coupling term
    α => 3.867e-7,   # Kerr nonlinearity
    ω => 1.4507941,  # pump frequency, resonant with antisymmetric mode (in paper, ħω0 + J)
    η => -0.08     # pumping leaking to site 2  (F2 = ηF1)
)
varied = F0 => range(0.002, 0.03, 50)

result = get_steady_states(harmonic_eq, varied, fixed)

A steady state result for 50 parameter points

Solution branches:   11
   of which real:    3
   of which stable:  2

Classes: stable, physical, Hopf, binary_labels

Let us first see the steady states.

p1 = plot(result, "u1^2 + v1^2", legend=false)
p2 = plot(result, "u2^2 + v2^2")
plot(p1, p2)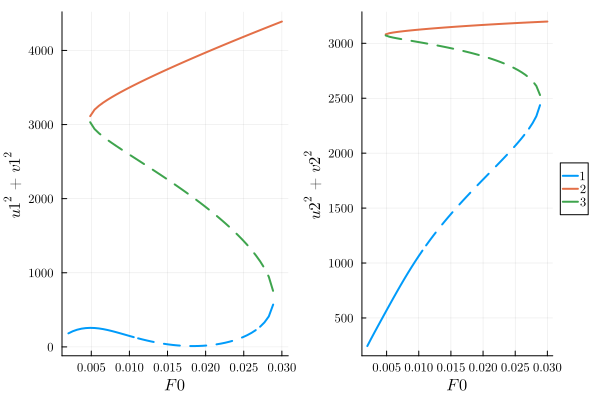

According to Zambon et al., a limit cycle solution exists around $F_0\cong 0.011$, which can be accessed by a jump from branch 1 in an upwards sweep of $F_0$. Since a limit cycle is not a steady state of our harmonic equations, it does not appear in the diagram. We do however see that branch 1 ceases to be stable around $F_0\cong 0.010$, meaning a jump should occur.

Let us try and simulate the limit cycle. We could in principle run a time-dependent simulation with a fixed value of $F_0$, but this would require a suitable initial condition. Instead, we will sweep $F_0$ upwards from a low starting value. To observe the dynamics just after the jump has occurred, we follow the sweep by a time interval where the system evolves under fixed parameters.

using OrdinaryDiffEqTsit5
initial_state = result[1][1]

T = 2e6
sweep = AdiabaticSweep(F0 => (0.002, 0.011), (0,T))

# start from initial_state, use sweep, total time is 2*T
time_problem = ODEProblem(harmonic_eq, initial_state, sweep=sweep, timespan=(0,2*T))
time_evo = solve(time_problem, Tsit5(), saveat=100);

Inspecting the amplitude as a function of time,

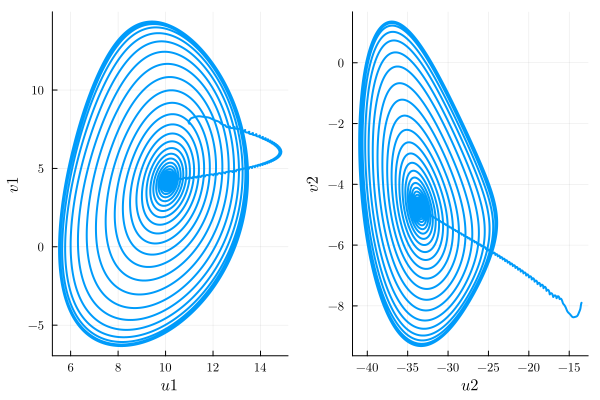
plot(time_evo, "sqrt(u1^2 + v1^2)", harmonic_eq)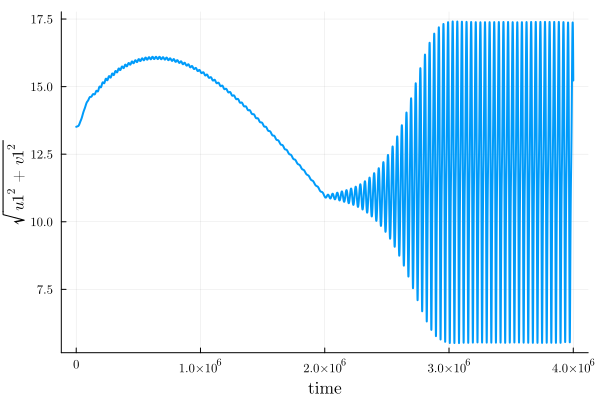

we see that initially the sweep is adiabatic as it proceeds along the steady-state branch 1. At around $T=2e6$, an instability occurs and $u_1(T)$ starts to rapidly oscillate. At that point, the sweep is stopped. Under free time evolution, the system then settles into a limit-cycle solution where the coordinates move along closed trajectories.

By plotting the $u$ and $v$ variables against each other, we observe the limit cycle shapes in phase space,

p1 = plot(time_evo, ["u1", "v1"], harmonic_eq)
p2 = plot(time_evo, ["u2", "v2"], harmonic_eq)
plot(p1, p2)